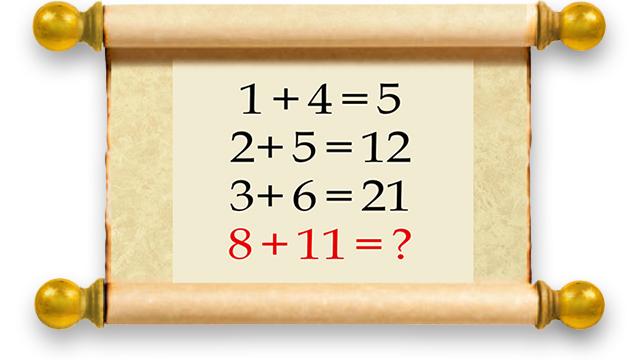Now some of you skeptics might be looking at this mind bender and thinking: “The answer is 19. It makes no difference that two of the previous equations are wrong.” And as far as we’re concerned, you’re correct in thinking that! If you declare 19 to be your answer, we’ll take it. That’s thinking outside of the box!
But for those who really want to test their metal, this mind bender has a few more tricks up its sleeve, as you'll see.