SPECIAL COVERAGE
Read More
Read More
Trump Advisers Meadows, Giuliani Among 18 Indicted in Arizona Election Case
The court documents also identified a ‘prior U.S. president.’
Trump Advisers Meadows, Giuliani Among 18 Indicted in Arizona Election Case
The court documents also identified a ‘prior U.S. president.’
Top Premium Reads
Top Stories
Most Read
A Peaceful Appeal for Freedom 25 Years Ago Still Echoes Today
About 10,000 people quietly congregated in Beijing on a spring day in 1999, now remembered as the April 25 appeal—the largest protest in China’s recent history.
Biden to Visit Syracuse to Tout New Investment in Chip Manufacturing
Micron will receive over $6 billion in government grants to boost domestic production.
Harvard Students Prop Up Tents to Protest Israel-Hamas War
Prime Minister of Israel Benjamin Netanyahu has called the ongoing pro-Palestinian protests across U.S. campuses ‘horrific.’
Shareholders, State Officials Allege Political, Religious Discrimination by Bank of America
‘This isn’t the right way to do business in America,’ Indiana State Treasurer Daniel Elliott stated.
Fauci to Testify in Public Hearing on COVID-19 Response, Origins
Dr. Fauci already testified in a closed door hearing and admitted there were serious systemic failures in the public health system during the COVID crisis.
RFK Jr.’s ‘Night of Laughter’ Illustrates Unconventional Fundraising Strategy
To compete with the deep pockets of the Biden and Trump campaigns, Mr. Kennedy employs non-traditional methods to generate money and awareness.
Columbia University Students React to House Speaker Mike Johnson’s Campus Visit
Mr. Johnson called for the resignation of Columbia University President Minouche Shafik.
Pentagon Watchdog Opens Probe of DOD Funds to China for Pathogen Research
Outraged lawmakers are demanding answers about American tax dollars going to firms controlled by the Chinese Communist Party.
Police Arrest Anti-Israel Protesters on University of Texas Austin Campus
Hundreds of students walked out of class to protest in support of Palestinians, demanding the university divest from Israel.
Editors' Picks
Judge Unseals Documents Showing FBI Discussed ‘Loose Surveillance’ of Trump’s Plane
A large tranche of documents were unsealed by Judge Aileen Cannon on Monday, revealing the FBI’s code name for the probe.
Newsom, Lawmakers Introduce Bill in Response to Arizona’s Abortion Ban
The measure would let Arizona doctors operate in California until Nov. 30, assuming Arizona voters will approve an abortion measure on their ballot.
‘Go Back to Class,’ Speaker Johnson Tells Protesting Students at Columbia University
The speaker said he would call the president to demand he send the National Guard to shut down the protests.
Georgia Governor Signs Anti-Squatter Law, Making It Easier for Homeowners ‘To Go After These Folks’
‘It is nothing short of insane that there are some who are entering other people’s homes and claiming them as their own,’ Georgia Gov. Brian Kemp said.

Mahler’s ‘Resurrection’ Symphony: Answering Nihilism
Mahler’s “Resurrection” Symphony is the musical equivalent of “Hamlet.” What led to its creation?
Mahler’s ‘Resurrection’ Symphony: Answering Nihilism
Mahler’s “Resurrection” Symphony is the musical equivalent of “Hamlet.” What led to its creation?
Epoch Readers’ Stories
A Nation Divided
Poem by an American Patriot
What Is Going on Here?
There are two major things plants need to survive and continue generating our life saving oxygen. The first is CO2, and the second is sunshine.
Wisdom From a Retired Cowboy Artist
I have lived the life of the sculptures I have made.
Inspired Stories
Empower the World with Your Story: Share Love, Inspiration, and Hope with Millions
Special Coverage
Special Coverage

Suffering Symptoms Caused By Prolonged Sitting? Try These 5 Exercises for Relief
Offsetting sitting with exercises throughout the day may alleviate and prevent pain and other consequences of prolonged sitting.

Suffering Symptoms Caused By Prolonged Sitting? Try These 5 Exercises for Relief
Offsetting sitting with exercises throughout the day may alleviate and prevent pain and other consequences of prolonged sitting.

‘Terrestrial Verses’: Censorship Up Close and Personal
Iranians face absurd suppression of their rights by bureaucrats.

Palazzo del Te: A Palace Near Mantua, Italy
In this installment of ‘Larger Than Life: Architecture Through the Ages,’ we visit a duke’s ‘pleasure palace.’

Robert Smalls: Navy Captain and Reconstruction-Era Politician
This former slave would not let anything stop him on the road to freedom.

How Art Is Helping Veterans With PTSD
Artist Tim Gagnon gives veterans a way to move forward in civilian life.

Jedidiah Morse: Father of American Geography
In this installment of ‘Profiles in History,’ we meet a minister who possessed a keen interest in geography and a concern about Christian liberalism.

How the US–Iraq Relationship Devolved Into War
Decades of animosity swirl in Steve Coll’s ‘The Achilles Trap: Saddam Hussein, the C.I.A., and the Origins of America’s Invasion of Iraq.'
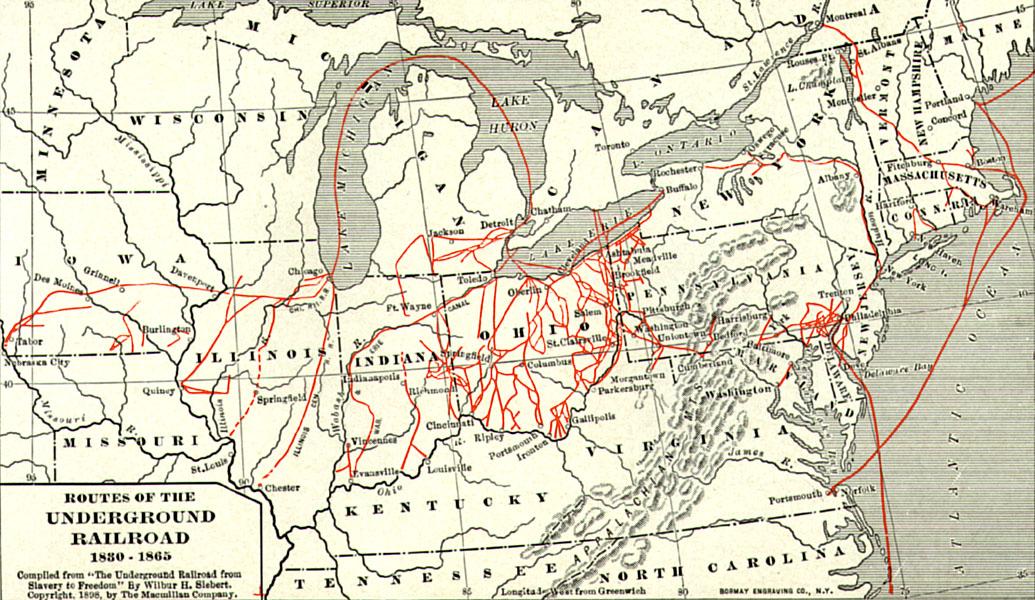
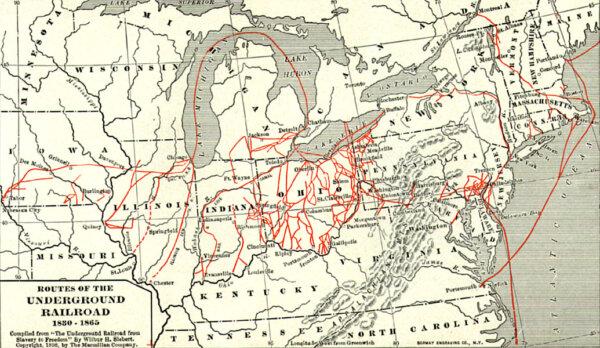
Important Players in a Divided Nation
Sons of the North, including young Spencer Kellogg, gave their all for the fight against slavery during the Civil War.

‘Terrestrial Verses’: Censorship Up Close and Personal
Iranians face absurd suppression of their rights by bureaucrats.

You Need a Kitchen Assistant
Your slow cooker can help you prepare a meal for less that two cents an hour.

Rocky Mountaineer Train Launches Summer Season Promising Spectacular Views
Rocky Mountaineer has four routes that will take passengers through Western Canada and the American Southwest.

After 5 Years of Closure, ‘Glamping’ Back Again in Yosemite National Park
Camping hopefuls can now enter a lottery to experience three of the five available campsites.

Ed Perkins on Travel: Solo Travel—Difficult but Improving
The travel industry is slowly making prices fair for true solo travelers.
Rocky Mountaineer Train Launches Summer Season Promising Spectacular Views
Rocky Mountaineer has four routes that will take passengers through Western Canada and the American Southwest.

























































![[PREMIERING APR 26, 7:00PM ET] Hope for Israel | Special Report](/_next/image?url=https%3A%2F%2Fimg.theepochtimes.com%2Fassets%2Fthemes%2Feet%2Fimages%2FEET_default_700x420.jpg&w=1200&q=75)






























































































![[LIVE Q&A 04/25 at 10:30AM ET] Why Is Australia Going After Elon Musk?](/_next/image?url=https%3A%2F%2Fimg.theepochtimes.com%2Fassets%2Fuploads%2F2024%2F04%2F24%2Fid5636785-CR-TN_REC_0425-600x338.jpg&w=1200&q=75)